Defeating Sudoku in five simple steps
I, like many others, have taken a liking to Sudoku puzzles. I started with some simple scanning techniques (examples 1-3) which worked with the easier puzzles. Angus Johnson’s Simple Sudoku program has a delightful Help containing many strategies to solving a puzzle. I haven’t got the hang of (or memorised) the most advanced techniques but recently I finished even the “Ultimate Challenges” in two Sudoku books (about 200 puzzles each) with the following strategies that I’ve found the most effective — and enough.
1. I always start a puzzle by looking at the smallest area possible which is the 3×3 square. I check the missing numbers starting from 1 and see if I can put a number anywhere.
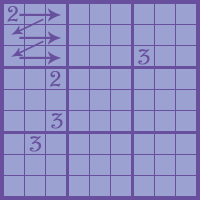
2. After I’ve gone through each of the 9 small squares so many times that I can’t add numbers anymore, I check each horizontal row.
3. After horizontal rows don’t help, I check each vertical row.
4. I repeat steps 1-3 until I can’t add any numbers. Then I write down the “candidates” in each square. Often this reveals new numbers to add when a square has only one possible candidate.
When the candidates are written down it’s easy to see pairs or small groups so I can strike out candidates in other squares. In the example there are three squares that have to contain the numbers 1,4, and 5 so I can discard them in the square that is outside the group. I do this scan on horizontal and vertical rows, too.
5. With the candidates in view it’s easy to find numbers to strike out when I go through the rows horizontally and vertically and notice that a number has to be contained in one of the 3×3 squares. Then I can strike out the number in the other 3×3 squares on the same row. Also, if a number is restricted to a 3×3 square and a vertical or horizontal row, candidates can be struck out within the 3×3 square.
In the example numbers 3, 6, and 9 have to be found on the first row so they can be struck out elsewhere in the second 3×3 square.
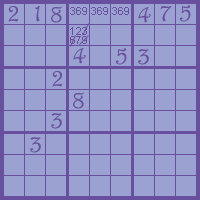
Before I learned the strategies 4 and 5 I had trouble finishing the tougher puzzles. I suppose I had thought of checking the pairs but not the larger groups.
Perhaps next I should take on making the puzzles because I tried that on Simple Sudoku and couldn’t get a single one pass the check (= only one solution).
Disclaimer: The examples are not trying to be realistic situations or solveable puzzles, they’re just diagrams.
Well, no, it’s not.)
).
Payday isn’t until October 10th so I had to take some money from my saving’s account (especially as I’ve been planning to buy the phone next week).